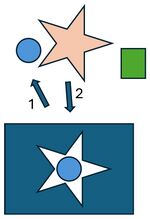
Convergent and Divergent Thinking
Convergent and divergent thinking are key skills required for critical thinking and problem solving. Convergent thinking quickly and efficiently uses tools, knowledge and reason to narrow down choices to reach an answer. Divergent thinking is somewhat the opposite. We typically start with a potential answer and work "backward" to find other, potentially better answers.
Convergent thinking is incredibly efficient, especially for problems with single definitive answers such as an algebra problem or parsing a sentence. As such, STEM education especially focuses on teaching us convergent thinking skills. It is an essential skill, as ALL problem-solving ends with convergent thinking when we decide on an answer to the question. And some classes of problems can be solved with only convergent thinking.
However, for most complex problems, such as those without a single definitive solution, convergent thinking can lead us to a less-than-ideal answer. Which isn't necessarily bad, BUT it can lead us to believe that our less-than-ideal answer is the single correct answer. We can see that happening right now in our national policies where complex problems are treated as if they have simple, single solutions. This is where divergent thinking is especially important at this point in time.
Examples of Convergent and Divergent Thinking
A good example of convergent/divergent thinking is the game infants play with shapes and holes. They have a circle, a square and a star. And a board with a star shaped hole. The infant will initially try each shape in each hole until one fits (trial and error). They might have to rotate the star multiple times until it actually fits. An experienced convergent thinker will use knowledge to immediately pick up the star and place it in the star-shaped hole with the correct orientation, all in one try. (In this case most all of this convergent thinking happens subconsciously.) Here, convergent thinking is more efficient than trying other choices. And, given a huge pile of circles and squares and one star, the efficiency quickly becomes apparent.
But now let's try again. In this case, we have lots of circles, squares and stars of varying sizes and one large square-shaped hole. Many of the shapes are small enough to fit inside the square hole. Only one square fits perfectly. Convergent may find a small circle that fits the square hole and stop there. Especially if they aren't aware of the other potential shapes and/or there are other problems competing for attention. Most real-world problems are like this: we don't know all the possible solutions, we find one that is good enough and we stop there. And we don't have unlimited time, we have lots of problems competing for our attention. In these situation, divergent thinking can be very useful; it helps us step back and recognize that there may be better solutions deserving of our attention. And together, convergent and divergent thinking help us modify the question and criteria from "find the shape that fits" to "find the shape that fits perfectly."
Humans are thus very adept at reducing complex questions to ones with definitive answers and therefore apply convergent thinking to all situations ("trying to fit a square peg in a round hole"). When we do this, we are unknowingly changing the question to fit the answer. As an example, ask football fans "who is the best quarterback", and most will answer definitively and cite criteria that supports their answer. Meanwhile another fan might give a different answer and cite different criteria. This approach makes evolutionary sense in that individuals are often forced to make quick "fight or flight" decisions and live with the consequences of that decision. Indecisiveness is not a good trait when faced with imminent danger.
Analogy: Birds-eye view vs. Close-up (Micro/Macro)
Very closely related is the ability to see a problem in detail from very close-up ("micro") as well as from afar ("macro"). Education tends to teach us to see things in detail. A doctor learns to treat a wound, a statistician knows how to calculate an average, a baker knows how to convert flour and water to bread. All essential skills. These professionals could not do their job without that detailed knowledge. All require convergent thinking skills.
But for more complex problems, there is great value in seeing a wider view. Additional insights can be gained, yielding better solutions when both are viewed. The statistician might benefit from knowing where the data came from and how the average will be interpreted, the baker might create new delicacies knowing what else is in the pantry. And this is even more important when we think in terms of societies, where others are involved. For example, an entrepreneur might create a glove that prevented the wound from ever happening, or a band-aid that allows a patient to avoid a trip to the doctor. A farmer may grow wheat with a higher gluten content for that baker. Doing so requires divergent thinking skills and a broader "holistic" view.
Critical AND Creative Thinking
So much of the focus of formal education, and what people think of as "critical thinking", is on convergent thinking. Which is good, because it is an essential skill. But that focus sometimes comes at the expense of recognizing the ability to think divergently, often see as "creative thinking."
And unfortunately, the ability to think critically and the ability to think creatively are often seen as opposites, and incompatible. A person is labeled as analytical or creative. One or the other. Science and Liberal Arts are often treated as opposites as opposed to complementary. We can see this in action today as Liberal Arts in colleges are being devalued and even questioned as important.
In Summary
Some problems can be solved with ONLY convergent/close-up thinking. Adding numbers, stitching a wound. And few problems can be solved ONLY with divergent/birds-eye thinking. And thus, this can lead divergent thinkers to the conclusion that convergent thinking is more important...and then to the conclusion that divergent thinking is unnecessary. Which is a good example of how convergent thinking alone can lead us to incorrect conclusions about complex problems. Because all innovation requires divergent thinking. The last step may be convergent, but the innovation could never have happened without divergent/creative thinking along the way. And our entire modern civilization is dependent on innovation.
To Learn More
Solving complex problems requires a continuous interchange between convergent and divergent thinking can become so seamless, so much a part of the process, that we don't even realize it is happening. In problem solving, we use convergent thinking to think of potential solutions, and divergent thinking to develop criteria and choose the best choice. "Thinking outside the box" and "brainstorming" are examples of methodologies to encourage divergent thinking.
Several popular frameworks for problem-solving are known by "CPS - Creative Problem Solving." The use of the word "creative" is there to emphasize the importance of divergent thinking in the process. And all emphasize the need for both divergent and convergent thinking throughout the process. Visit the Problem Solving Frameworks page for more detail.